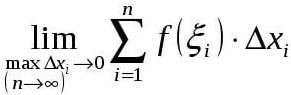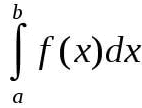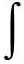Интегра́льное исчисле́ние - раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения к решению различных математических, физических и других задач. В систематической форме интегральное исчисление было предложено в XVII в. И. Ньютоном и Г. Лейбницем. Интегральное исчисление тесно связано с дифференциальным исчислением; интегрирование (нахождение интеграла) есть действие, обратное дифференцированию: по данной непрерывной функции f(x) ищется функция F(x) (первообразная), для которой f(x) является производной. Вместе с(х) первообразной функцией для f(x) является и f(x) + С, где С - любая постоянная. Общее выражение F(х) + С первообразных непрерывной функции f(x) называется неопределённым интегралом; он обозначается
∫f(x)dx = F(х) + С.
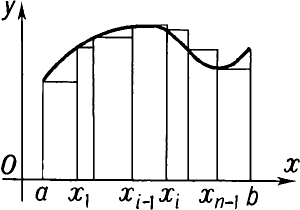
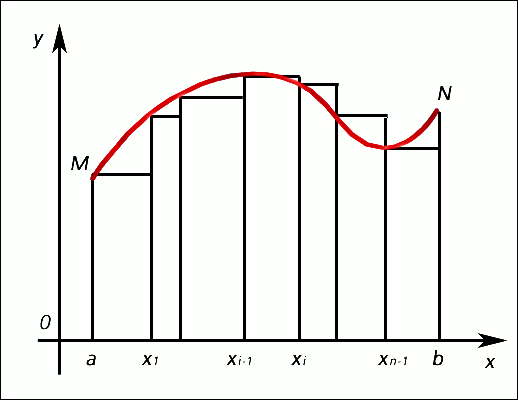
Определённым интегралом непрерывной функции f(х) на отрезке [а, b], разделённом точками x1, х2,..., xn-1, называется предел интегральных сумм 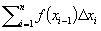 , где Δхi = xi - xi-1, при условии, что наибольшая разность Δxi стремится к нулю и число точек деления неограниченно увеличивается; его обозначают
, где Δхi = xi - xi-1, при условии, что наибольшая разность Δxi стремится к нулю и число точек деления неограниченно увеличивается; его обозначают  ">Кратный интеграл, Криволинейный интеграл, Поверхностный интеграл).
">Кратный интеграл, Криволинейный интеграл, Поверхностный интеграл).
">
* * *
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ - ИНТЕГРА́ЛЬНОЕ ИСЧИСЛЕ́НИЕ, раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения к решению различных математических, физических и других задач. В систематической форме интегральное исчисление было предложено в 17 в. И. Ньютоном и Г. Лейбницем. Интегральное исчисление тесно связано с дифференциальным исчислением (см. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ); интегрирование (нахождение интеграла) есть действие, обратное дифференцированию: по данной непрерывной функции f(x) ищется функция F(x) (первообразная), для которой f(x) является производной. Вместе с F(x) первообразной функцией для f(x) является и F(x) + C, где С - любая постоянная. Общее выражение F(x) + C первообразных непрерывной функции f(x) называется неопределенным интегралом; он обозначается
Определенным интегралом непрерывной функции f(x) на отрезке [a, b], разделенном точками (рис.), называется предел интегральных сумм , где , при условии, что наибольшая разность стремится к нулю и число точек деления неограниченно увеличивается; его обозначают (самый знак возник из первой буквы S латинского слова Summa). Через определенные интегралы выражаются площади плоских фигур, длины кривых, объемы и поверхности тел, координаты центров тяжести, моменты инерции, работа, производимая данной силой, и т. д. О связи между определенным интегралом и первообразной см. -Ньютона Лейбница формула (см. НЬЮТОНА-ЛЕЙБНИЦА ФОРМУЛА). Понятие интеграла распространяется на функции многих переменных (см. Кратный интеграл (см. КРАТНЫЙ ИНТЕГРАЛ), Криволинейный интеграл (см. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ), Поверхностный интеграл (см. ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ))
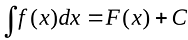 .
.